This is just to reinforce today’s lecture. The idea is that many concepts:
- The limit of \(f(x)\) of a limit at \(x = a\),
- The continuity of \(f(x)\) at \(x= a\),
- The differentiability of \(f(x)\) at \(x=a\),
- The point \(a\) being a local maximum of \(f(x)\)
Only depend on the behavior of \(f(x)\) in a region \((a-\delta,a+\delta)\) for any \(\delta\).
But is there anything that is not a “local” property of a function?
Here local means some fact that can really be detected in one of these very small neighbourhoods of \(a\). One property is being a maximum (not must a local maximum). Remember that we proved the following:
Theorem: If \(f(x)\) is continuous on a closed interval \([a,b]\), then \(f(x)\) obtains a maximal value. That is, there exists a \(c \in [a,b]\) so that \(f(c) \ge f(x)\) for all \(x \in [a,b]\).
To prove this theorem, we really had to exploit not only continuity but also some extra properties of the real numbers, namely that any non-empty bounded set \(A\) has a least upper bound \(\mathrm{sup}(A)\). One reason why it is hard to prove is that we had to use local properties of continuity to establish something on the entire interval (which by contrast we call a global property). Leaving that aside, the property of being a maximum value is not a local property. That is, suppose you have a differentiable function \(f(x)\) on an interval \([a,b]\), and you know the behavior of the function \(f(x)\) around a point \(c\). On Friday, we will prove the following:
Theorem: If \(f(x)\) is differentiable at \(c\) and \(c\) is a local maximum of \(f(x)\), then \(f'(c)=0\).
However, something we can not do is tell whether \(c\) is actually a maximum of \(f(x)\) on the entire interval just by looking at the behavior around \(x =c\). This is hopefully intuitive, but let’s give an example. Consider the following three functions:
\[\begin{aligned}
a(x) & = 3 x^4 – 20 x^3 + 36 x^2, \\
b(x) & = 12 x^4 – 80 x^3 + 162 x^2 – 108 x + 33, \\
c(x) & = \begin{cases} a(x), & x < 1, \\
b(x), & x \ge 1. \end{cases} \end{aligned}\]
Here is the graph of \(a(x)\) in blue and \(c(x)\) in orange:
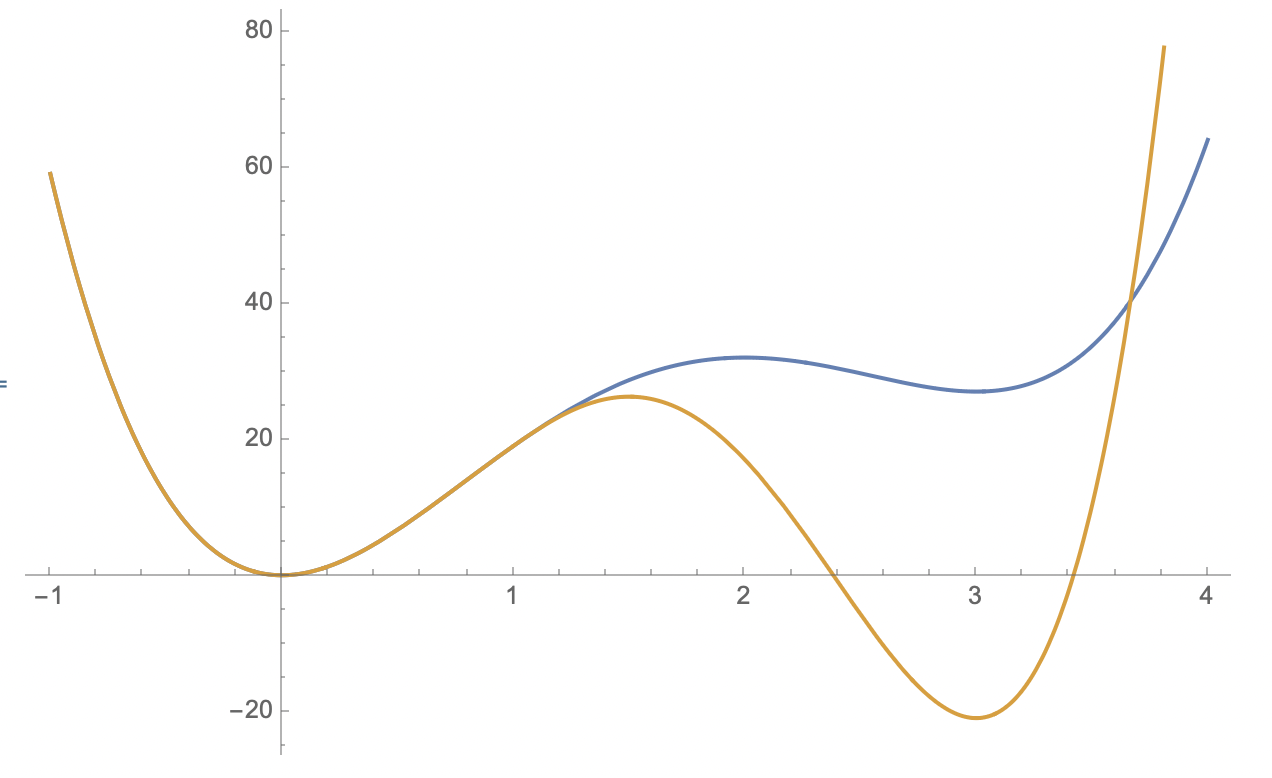
I claim that the three functions \(a(x),b(x),c(x)\) are all differentiable. This should be clear for \(a(x)\) and \(b(x)\). For \(c(x)\) it follows from the local principle above except for the point \(x=1\). Note that
\[c(1) = b(1) = 12-80+162-108+33= 19 = 3 – 20 + 36= a(1).\]
To check that \(c(x)\) is differentiable we check that the right and limits both exist and they are both equal. We have
\[\lim_{h \rightarrow 0^{+}} \frac{c(1+h) – c(1)}{h} =
\lim_{h \rightarrow 0^{+}} \frac{b(1+h) – b(1)}{h} = b'(1) = 24.\]
On the other hand, since \(b(1)=a(1)\), we have
\[\lim_{h \rightarrow 0^{-}} \frac{c(1+h) – c(1)}{h} =
\lim_{h \rightarrow 0^{-}} \frac{a(1+h) – a(1)}{h} = a'(1) = 24.\]
The point is that the right and left hand side limits only involve \(a(x)\) or \(b(x)\), and because those functions are differentiable we can compute the limits in terms of those functions and their derivatives. Now let us check the critical points of \(a(x)\), \(b(x)\), and \(c(x)\). We have
\[\begin{aligned} a'(x) & = 12 (-3 + x) (-2 + x) x, \\
b'(x) & = 12 (-3 + x) (-3 + 2 x) (-1 + 2 x) \end{aligned}.\]
Since \(a'(1)=b'(1) = 24\), we get
\[c'(x) = \begin{cases} 12 (-3 + x) (-2 + x) x, & x < 1 \\ 12 (-3 + x) (-3 + 2 x) (-1 + 2 x), & x \ge 1. \end{cases}\] What are the critical points? We get:
- The critical points of \(a(x)\) are \(x = 0,2,3\).
- The critical points of \(c(x)\) are \(x=0,3/2,3\).
We now (finally) get the the point. The functions \(a(x)\) and \(c(x)\) are the same function in a neighbourhood of \(x=0\). So we deduce:
- The functions \(a(x)\) and \(c(x)\) have the same value at \(x = 0\), and the same derivative at \(x=0\).
- The point \(x = 0\) is a local minimum for \(a(x)\) and \(c(x)\).
However, the function \(a(x)\) has its mimimum for all \(x\) at \(x=0\), whereas the function \(c(x)\) does not, it’s minimum occurs at \(x=3\). There is no way to tell this just by looking at these functions around \(x=0\).
